Matrices Especiales

Matrices Especiales 

MATRICES

Una matriz es un arreglo bidimensional compuesto de elementos ubicados en filas (i) y columnas (j), siendo para i los valores de m y para j los valores de n.

i(m), j (n)

MATRICES ESPECIALES

MATRIZ IDENTIDAD

Es aquella que posee el mismo número de columnas y filas. La diagonal está conformada por valores de uno (1) y las demás posiciones contienen valores cero (0). Se representa como In, donde n es la dimensión de la matriz.

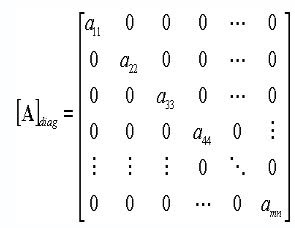
MATRIZ DIAGONAL

Es aquella cuyos elementos son nulos, pero con valores en la diagonal. Aplica para las matrices con igual número de filas y columnas. Se denota por la expresión A= diag (v, m * n) , donde v corresponde al vector y m*n a la dimensión de la Matriz.

MATRIZ TRIANGULAR

Existen dos tipos de matrices triangulares:

Triangular superior

Aquella cuyos elementos que están por debajo de la diagonal de la matriz son iguales a 0

Triangular inferior

Aquella cuyos elementos que están por encima de la diagonal son iguales a 0

MATRIZ TRASPUESTA

Es una matriz de dimensión m * n que tiene por columnas a las filas de la matriz.

Se denota como At

MATRIZ ADJUNTA

Es la matriz que resulta de quitar la fila i y la columna j de A. Se denota por la fórmula

MATRIZ SIMÉTRICA

Es aquella cuyos valores son iguales a su traspuesta

Diremos que una matriz A de orden mxn es una matriz simétrica si coincide con su traspuesta, es decir A=A`
Es evidente que las matrices simétricas tienen que ser matrices cuadradas.